OpenGL (Open Graphics Library este o specificație a unui standard care definește un

API (Application Programming Interface) multiplatformă foarte utilizat pentru programarea componentelor grafice 2D și 3Dale programelor de calculator. Interfața constă în peste 250 de apeluri diferite care folosesc la a desena pe ecranul calculatorului scene 3D complexe din primitive (din primitives, elemente simple).

OpenGL a fost inițial dezvoltat de compania Silicon Graphics, Inc. (SGI) în 1992 și este foarte utilizat în grafică asistată de calculator, realitate virtuală, vizualizare științifică, simulări de zboruri sau jocuri pe calculator. Acest ultim domeniu este în strânsă competiție cu tehnologia DirectX de la Microsoft (compară OpenGL cu Direct3D). Proiectul OpenGL este condus de compania Khronos Group, un consorțiu tehnologic non-profit.

Imagine similarÄƒ

http://www.academic.ro/ebook/profesor/html-cap1/opengl/lectii/opengl.html

Functii grafice în mediul OpenGL

I. Ordinea operatiilor

Definirea formelor geometrice "primitive", adica descrierea geometrica a obiectelor.
Aranjamentul spatial, tri-dimensional, al obiectelor si alegerea unui punct avntajos pentru observarea scenei.
Calculul culorii obiectelor. Culoarea poate fi calculata (determinata) prin program, de exemplu datorita reflexiei luminii, sau atribuita unic cu ajutorul unei "texturi" (un desen arbitrar, asemanator unei tesaturi, sau tip de hasuri).
Conversia descrierii matematice a obiectelor în informatie color catre ecran. Procesul este numit rasterizare.
Pe parcursul acestor operatii, mediul grafic executa aceste operatii împreuna cu eliminarea partilor invizibile din scena, ascunse de alte obiecte.

II. Organizarea programului pentru utilizarea OpenGL

Un program obisnuit în mediul OpenGL începe cu deschiderea unei ferestre grafice, care se adreseaza memoriei grafice a calculatorului si descrie un cadru de imagine pe monitor.

Urmeaza apoi instructiuni pentru alocarea contextului GL care este asociat unei ferestre grafice. Din acest punct, programatorul poate elabora programul propriu-zis, asociat ferestrei respective, proprii mediului OpenGL. Cele mai simple comenzi sunt asociate trasarii unor obiecte geometrice simple, puncte, linii, poligoane, în timp ce altele permit în plus redarea (engl. rendering) acestor primitive împreuna cu aspectul creat de variatiile de culoare si luminozitate determinate de pozitia si caracteristicile sursei de lumina precum si de poxitia observatorului.

Mai exista si apeluri adreste exclusiv memoriei grafice aferente unui cadru de imagine pe monitor, cum ar fi citirea si scrierea unui pixel.

wpe48.jpg (65945 bytes)

Ultima operatie (swap buffers) este în mod special necesara pentru continuitatea animatiei. Se folosesc doua fisiere tampon pentru imaginea de pe ecran. In timp ce unul este folosit pentru afisaj, celalalt este folosit pentru desenarea cadrului de imagine urmator.

III. Bucla de evenimente (Event Loop)

Programele OpenGL lucreaza într-o bucla de evenimente, de obicei infinita, adica se asteapta o actiune exterioara cum ar fi apasarea unei taste, actiunile mouse-lui, etc.

Redimensionarea scenei are loc la fiecare redimensionare a ferestrei. Afisarea ferestrei are loc la prima desenare sau atunci când fereastra este adusa în planul apropiat.

IV. Sintaxa comenzilor OpenGL

Comenzile OpenGL folosesc prefixul gl , cuvintele din comanda sunt separate prin semnul _ iar prima litera din cuvânt este o majuscula, de exemplu glBegin(). Similar, constantele sunt definte dupa aceleasi reguli, de exemplu GL_COLOR_BUFFER_BIT. Câteva comenzi OpenGL mai au la sfârsit un numar sau 1-3 litere care semnifica numarul si tipul parametrilor comenzii. Primul caracter indica numarul valorilor tipului indicat care trebuie cotinut în comanda. Al doilea caracter sau pereche de caractere indica tipul argumentelor (întregi sau reale). Ultimul caracter, daca este vindica ca comanda poate sa se refere la un vector în loc de un scalar. De exemplu, în comanda glVertex3fv(), 3 este folosit pentru a indica trei argumente, f este folosit pentru a indica tipul de date real iar v indica tipul vectorial.

Standardizarea acestora este urmatoarea:

Numarul de argumente: 2, 3, sau 4
Tipuri de date::

`f' float
`d' double float
`s' signed short integer
`i' signed integer
`b' character
`ub' unsigned character
`us' unsigned short integer
`ui' unsigned integer
Format: `v' indica formatul vector. Absenta lui `v' indica un scalar

Pentru prezentarea generala a comenzilor, aceste specificatii pot fi ignorate iar comanda este scrisa folosind sufixul * în locul lor, cum ar fi glColor*().

V. Primitive în limbajul OpenGL

Programatorului I se ofera urmatoarele primitive (si cuvintele cheie asociate) pentru construirea obiectelor:

Imagini pentru grafica pe calculator primitive

Fiecare obiect geometric este descris printr-un set de vârfuri (vertex-uri) si tipurile de primitive care urmeaza sa fie trasate. Tipul primitivei alese determina daca vârfurile sunt conectate sau nu. Observati ca în limbajul POV, sunt definite în plus câteva obiecte uzuale, cum ar fi cilindru,sfera, etc.

Deci, în OpenGL, toate obiectele sunt decrise ca un set de vertexuri ordonate în spatiu Comanda glVertex*() este folosita pentru a defini un vertex. Exemple de folosire:

 glVertex2s(1, 2);
 glVertex3d(0.0, 0.0, 3.1415926535898);
 glVertex4f(1.3, 2.0, -4.2, 1.0);
 GLdouble vector[3] = {3.0, 10.0 2033.0};
 glVertex3dv(vector);

Toate aceste structuri trebuie incluse între începutul (glBegin()) Si sfârsitul (glEnd()) structurii de reprezentare. Desenarea se face atunci cand este întâlnita instructiunea glBegin(), cu exceptia cazurilor acoperite de lista de afisaj (DisplayList: glEnd()) care vor fi discutate mai jos.

Este important de observat aspectul comenzilor OpenGL care nu sunt executate imediat ce sunt întâlnite. Este necesaracomanda glFlush() pentru a ne asigura de aceasta la sfârsitul secventei de desenare

VI. Schimbarea starii

Atunci când sunt trasate primitivele, fiecare este afectata de variabilele de "stare", cum ar fi: grosimea liniei, culoarea, metoda de hasurare. Unele variabile de stare se refera la aspectul scenei. Acestea pot avea valori implicite (default values) si valori logice (fals: GL_FALSE sau adevarat: GL_TRUE). Alte variabile de stare se refera la o lista definita de Glenum. Unele valori pot fi de tip întreg sau real (GLfloat, GLint, etc.).

Fiecare variabila de stare are o valoare implicita (default value), care poate fi modificata prin program.

Variabilele de stare "On"-activat si "Off"-dezactivat

Variabilele de stare în OpenGL pot fi activate sau dezactivate cu comenzile glEnable(GLenum capability) si respectiv glDisable(GLenum capability) unde constantele simbolice indica o posibilitate a limbajului.

Valoarea curenta a unei variabile de stare poate fi verificata prin folosirea comenzii glIsEnabled(GLenum capability) care ia valorile GL_TRUE sau GL_FALSE.

Câteva posibilitati ale mediului sunt:

GL_POINT_SMOOTH

Daca este activata, functia confera unui punct un aspect neted,altfel marginile acestuia vor fi bine definite (engl. aliased)

GL_LINE_SMOOTH
Similar pentru o linie

GL_LINE_STIPPLE
Daca este activata, functia foloseste aspectul predefinit pentru o linie.

Modurile variabilelor de stare

Modurile variabilelor de stare implica comenzi specifice, un exemplu fiind nuanta, data de GL_SHADE_MODEL.

O linie sau un poligon pot fi trasate sau hasurate cu o singura culoare sau cu o paleta de culori, asemanatoare curcubeului (engl. smooth shading, sau Gouraud Shading). Hasurarea dorita se poate efectua cu comanda glShadeModel(GLenum mode) unde mode poate fi GL_SMOOTH pentru hasurare cu paleta sau GL_FLAT pentru hasurare cu o singura culoare.

Valorile variabilelor de stare

Valorile variabilelor de stare pot fi aflate si schimbate prin program. Tipic pot fi folosite comenzile urmatoare, în functie de scopul urmarit: glGetBooleanv(), glGetDoublev(), glGetFloatv(), sau glGetIntegerv().

Culoarea

Maniera cea mai obisnuita de schimbare a culorii este folosirea definitiei RGB glColor3f(GLfloat red, GLfloat green, GLfloat blue) unde red, green, si blue sunt valori reale cuprinse între 0 si 1. Valoarea 0.0 corespunde unei contributii minime a culorii de baza folosite iar 1.0 unei contributii maxime.

Negru glColor3f(1.0, 0.0, 0.0)

Rosu glColor3f(0.0, 1.0, 0.0)

Verde glColor3f(0.0, 0.0, 1.0)

Albastru glColor3f(1.0, 1.0, 0.0)

Galben glColor3f(0.0, 1.0, 1.0)

Cian glColor3f(1.0, 0.0, 1.0)

Magenta glColor3f(1.0, 1.0, 1.0)

Alb glColor3f(0.0, 0.0, 0.0)

Fisierul tampon trebuie golit de fiecare data când construim o scena, folosind comanda glClear(GL_COLOR_BUFFER_BIT).

Dimensiunea unui punct

Dimensiunea unui punct redat este data de comanda glPointSize(GLfloat size) unde size este dimensiunea în pixeli. Numarul trebuie sa fie mai mare decât 0, iar valoarea implicita este 1.0.

Grosimea liniei

Pentru controlul grosimii unei linii folosim comanda glLineWidth(GLfloat width) unde width este latimea dorita exprimata în pixeli. Latimea trebuie sa fie mai mare eecât 0.0 iar valoarea implicita este 1.0.

Linia întrerupta

Pentru construirea unei linii întrerupte, aspectul este declarat folosind comanda glLineStipple(GLint factor, GLushort pattern) unde pattern este o serie de 16 valori binare, 0 si 1, repetate pentru a codifica aspectul liniei. Valoarea 1 indica penita jos iar valoarea 0 indica penita sus. Aceasta secventa poate fi apoi alterata folosind un factor, care multiplica aceasta serie. Acest factor ia valori cuprinse între 0 si 255.. Variabila de stare GL_LINE_STIPPLE trebuie activata prin apelarea instructiunii glEnable(GL_LINE_STIPPLE).

VII. Construirea scenelor

Intr-o scena 3 dimensionala, obiectele din planul apropiat le pot acoperi pe cele din planul departat. De aceea, pentru o redare realista, trebuie îndepartate din desen suprafetele ascunse. Operatia este efectuata de doua fisiere(sau zi°one de memorie) tampon, pentru adâncime si respectiv pentru testarea adâncimii. La desenare, se asociaza fiecarui pixel o valoare pentru adîncime care este stocata în fisierul tampon de adîncime. Pentru fiecare vertex din scena este efectuat un test de adâncime, pentru a stabili daca nu cumva un vertex deja desenat acopera vertexul curent.

Fisierele tampon de adâncime trebuie activate folosind comanda glEnable(GL_DEPTH_TEST) iar înainte de reprezentarea scenei tamponul de adâncime trebuie golit cu comanda glClear(GL_DEPTH_BUFFER_BIT). Mediul OpenGL traseaza implicit poligoane în care toti pixelii din interior au o anumita culoare, însa poligoanele pot fi trasate si prin folosirea liniilor sau folosind puncte pentru reprezentarea vârfurilor. In OpenGL, un poligon are doua fete care pot avea culori diferite, dupa dorinta, pentru a permite vizualizarea sectiunilor.

Comanda glPolygonMode(GLenum face, GLenum mode) controleaza modul de trasare a fetelor poligonului. Parametrul face poate fi GL_FRONT (fata), GL_BACK(dos), sau GL_FRONT_AND_BACK (ambele); mode poate fi GL_POINT, GL_LINE, sau GL_FILL pentru a indica daca poligonul este reprezentat în puncte, linii sau ca o suprafata colorata. Valoarea implicita este ca mbele fete sunt colorate.

Un poligon colorat poate avea o anumita hasura, data de comanda glPolygonStipple(const GLubyte *mask) unde argumentul mask este un pointer catre o matrice imagine (bitmap) cu dimensiunea 32x32 care este interpretata ca o masca cu valorile 0 si 1. Variabila de stare GL_POLYGON_STIPPLE trebuie activata cu comanda glEnable(GL_POLYGON_STIPPLE).

Comanda glCullFace(GLenum mode) indica poligoanele ce trebuie ignorate din reprezentare, înaintea tribuirii unor coordonate planare pentru trasarea pe ecran. Parametrul mode poate fi parametrizat cu GL_FRONT, GL_BACK, sau GL_FRONT_AND_BACK pentru a indica fata, dosul sau amândoua pentru poligonul în discutie.

VIII. Vizualizarea si modelarea transformarilor

Vizualizarea transformarilor este analoaga cu pozitionarea si orientarea camerei de luat vederi. Modelarea transformarilor este anloaga cu pozitionarea si orientarea obiectelor sa modelului în scena. In OpenGl, vizualizarea trebuie sa preceada modelarea.

Transformarile sunt efectuate prin folosirea matricilor. La orice moment pot fi modificate urmatoarele matrici:

matricea de vizualizare
matricea de proiectie
matricea de textura (continând hasurile)

Variabila de stare GL_MATRIX_MODE specifica matricile modificabile. Valoarea implicita este matricea modelului.

Comanda glMatrixMode(GLenum mode) este folosita pentru a schimbavaloarea variabilei de stare GL_MATRIX_MODE.. Valorile posibile ale argumentului de modelare sunt GL_MODELVIEW, GL_PROJECTION, si GL_TEXTURE. La apelarea functiei glMatrixMode() sunt afectate toate comenzile ulterioare pentru transformarea matricii respective. Comanda glLoadIdentity() este folosita pentru a transforma matricea modificabila într-o matrice unitate. Comanda glTranslate(TYPE x, TYPE y, TYPE z) multiplica matricea modificabila curenta cu o matrice care misca obiectul cu valori specificate x, y si z (adica modifica coordonatele locale curente cu valorile x, y si z).

Comanda glRotate(TYPE angle, TYPE x, TYPE y, TYPE z) multiplica matricea modificabila (sistemul de referinta al obiectului) cu o matrice de rotatie în sensul invers acelor de ceasornic în jurul axei care trece prin origine si coordonatele curente x,y,z. Parametrul angle specifica unghiul de rotatie în grade.

Comanda glScale(TYPE x, TYPE y, TYPE z) multiplica matricea modificabila cu o matrice de deformare, care permite micsorarea, marirea sau oglindirea obiectului de-a lungul axelor. Fiecare coordonata x, y, si z a fiecarui punct din obiect este multiplicata cu o valoare corespunzatoare din matricea de transformare.

IX. Transformari asupra planului de vizualizare

Aceste transformari sunt analoage alegerii dimensiunii imaginii. OpenGL ia ca valori implicite dreptunghiul determinat de fereastra programului. Comanda glViewport(GLint x, GLint y, GLsizei width, GLsizei height) este folosita pentru schimbarea dimensiunii dreptunghiului folosit pentru trasare. Parametrii x si y specificacoltul stanga sus al dreptunghiului, iar width si height sunt latimea si respectiv înaltimea acestuia.. Aceasta comanda este folosita în special pentru modificarea scenei în cazul modificarii dimensiunii ferestrei de catre utilizator.

X. Perspectiva

In proiectia de perspectiva, volumul de vizualizare are forma unui trunchi de con (engl. frustum), adica, cu cât un obiect este mai departat de camera de luat vederi, cu atât este mai mic în imagine. Aceasta functie este realizata cu comanda glFrustum(GLdouble left, GLdouble right, GLdoublebottom, GLdouble top, GLdouble near, GLdouble far). Argumentele left si right specifica the coordonatele pentru planele de delimitare a perspectivei din stânga si dreapta. Argumentele bottom si top specifica coordonatele planelor de limitare podea si tavan. Argumentele near si far specifica distantele pâna la planele cel mai apropiat si respectiv cel mai îndepartat. Ambele distante trebuie sa fie pozitive.

XI. Proiectia ortografica

In proiectia ortografica, volumul de vizualizat are forma unei cutii. Spre deosebire de proiectia ortografica, volumul de vizualizat nu se schimba de la un colt la altul si prin urmare distanta camera-obiect nu schimba dimensiunile aparente ale obiectului în imagine.

Comanda este glOrtho(GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble far). Argumentele left si right specifica coordonatele stânga si dreapta ale paralelipipedului de proiectie, iar bottom si top pentru planele podea si respectiv tavan. Argumentele near si far specifica pozitiile planelor apropiat si respectiv îndepartat ale paralelipipedului. Distantele negative sunt situate în spatele observatorului (camerei de luat vederi).

XII. Liste de afisaj (engl. Display Lists)

O lista de afisaj este un grup de comenzi OpenGL care sunt pregatite pentru executie ulterioara. Atunci când invocam lista de afisaj, comenzile prestabilite vor fi executate în ordinea prescrisa

O utilizare comuna este crearea unei liste de afisaj pentru un obiect care urmeaza sa fie desenat de mai multe ori. Daca trebuie calculate doar vertexurile acestuia, timpul de calcul este multa mai mic decât pentru întreaga scena.

Comenzile glNewList(GLuint name, GLenum mode) si glEndList() sunt folosite pentru crearea începutului si respectiv sfârsitului unei astfel de liste. Argumentul mode specifica modul de compilare, care poate fi:

GL_COMPILE, care înseamna ca urmatoarele comenzi NU vor fi executate în ordinea specificata în lista, sau

GL_COMPILE_AND_EXECUTE, care specifica obligativitatea executarii conform listei

Dupa ce lista a fost creata, ea poate fi executata cu comanda: glCallList(GLuint name).

XIII. Animatia

Animatia în grafica pe calculator este obtinuta prin utilizarea celor doua fisire tampon mentionate mai sus. Prin aceasta avem la dispozitie doua cadre color complete, pregatite pentru afisaj. Intimp ce un cadru este afisat, celalalt este desenat. La sfârsit, cele doua cadre sunt interschimbate si începe reprezentarea noului cadru (3) peste cadrul (1) samd.

OpenGL nu ofera nici o comanda standard pentru interschimbarea fisierelor tampon, aceasta sarcina revenindu-i sistemului de operare. Comanda care specifica modificarea este glFlush().

XIV. Iluminarea scenei

In OpenGL exista doua feluri de surse de lumina: directionala si pozitionala. O sursa directionala este situata la o distanta infinita fata de scena (creaza un fascicul paralel) în timp ce sursa pozitionala este situata aproape sau chiar înauntrul scenei. Sub aspectul eficientei calculului, o sursa pozitionala este mai eficienta decât cea directionala, datorita mai ales numarului mai mic de obiecte întâlnite. Comanda glLightfv() poate fi folosita pentru specificarea pozitiei sursei de lumina si daca ea este directionala sau pozitionala. Se mai pot specificavalorile componentelor de culoare ale sursei, cum ar fi: "ambient color", "diffuse color", "specular color", "emissive color", "shininess". Dupa ce sursele de lumina au fost definite, mai trebuie specificati vectorii normali si proprietatile obiectelor scenei. Vectorii normali ai unui obiect definesc orientarea sa relativ la sursa de lumina. Vectorii normali pot fi specificati pentru fiecare vertex sau aranjament de vertexuri. Comanda folosita este: glNormal(). Componentele de culoare alese pentru sursele de lumina au semnificatii diferite fata de cele ale materialelor. Pentru sursele de lumina, numerele corespund unui procentaj fata de lumina alba. Prin urmare, cea mai stralucitoare sursa are valorile (1.0, 1.0, 1.0). Pentru materiale, numerele corespund reflectivitatii suprafetei vertexurilor. Pentru materiale se foloseste comanda glMaterialfv(), în care se introduc valorile caracteristice materialului.

Comanda glColorMaterial() are scopul scaderii timpului de calcul în cazul schimbarii proprietatilor materialului si trebuie utilizata de fiecare data când se modifica o caracteristica oarecare a materialului. Orice schimbare a culorii curente poate fi facuta prin apelarea functiei glColor() care actualizeaza imediat proprietatea de material specificata de glColorMaterial(). Variabila de stare GL_COLOR_MATERIAL trebuie activata cu comanda glEnable(GL_COLOR_MATERIAL). Activarea iluminarii se face cu comanda glEnable(GL_LIGHTING) si pentru fiecare sursa de lumina din scena se foloseste glEnable(GL_LIGHTi) unde GL_LIGHTi este numarul curent al sursei.

https://www3.ntu.edu.sg/home/ehchua/programming/opengl/CG_Introduction.html

http://www.csc.villanova.edu/~mdamian/Textbooks/opengl_programming_guide_8th_edition.pdf

https://www3.ntu.edu.sg/home/ehchua/programming/opengl/CG_Introduction.html

TUTORIAL

VIDEO

1. https://www.youtube.com/watch?v=qniXE1wi0Po
2. https://www.youtube.com/watch?v=Oa5RWmR2OvI

Know some C++? Want to learn how to program in 3D? You've come to the right place! Designed to be understandable to beginners, but advanced enough for experienced developers, the free video tutorials here will get you started making 3D programs using OpenGL and GLUT in no time. Each lesson has a text version and comes with exercises to help you gain experience programming on your own, rather than just shoving lots of syntax down your throat. So what are you waiting for? Let's learn some OpenGL!

[Actual clip from lesson 21]

SCRISE

http://www.cs.ubbcluj.ro/~per/Grafica/L_T/curs02.htm http://old.unibuc.ro/prof/vlada_m/docs/2011/apr/11_12_12_01OpenGL_Programming_Guide.pdf
http://gta.math.unibuc.ro/stup/suport_curs_CGGC.pdf

Follow them in the right order !

Tutorial 1 : Opening a window

Tutorial 2 : The first triangle

Tutorial 3 : Matrices

Tutorial 4 : A Colored Cube

Tutorial 5 : A Textured Cube

Tutorial 6 : Keyboard and Mouse

Tutorial 7 : Model loading

Tutorial 8 : Basic shading

Follow them in any order

Tutorial 9 : VBO Indexing

Tutorial 10 : Transparency

Tutorial 11 : 2D text

Tutorial 12 : OpenGL Extensions

Tutorial 13 : Normal Mapping

Tutorial 14 : Render To Texture

Tutorial 15 : Lightmaps

Tutorial 16 : Shadow mapping

Tutorial 17 : Rotations

Tutorial 18 : Billboards & Particles

FAQ

Contribute

Translation

Math Cheatsheet

Useful Tools & Links

An FPS counter

Building your own C application

Clicking on objects

Implementări

Mesa 3D

Design

A Graphics Pipeline Process

OpenGL are două scopuri principale:

să mascheze (ascundă) complexitatea interfețelor cu diferite acceleratoare 3D, prin confruntarea programatorului cu un singur API uniform.
să mascheze capabilitățile diferitelor platforme hardware, prin cerința ca toate implementările să accepte OpenGL ca un set complet (cu ajutorul emulării de software, dacă este necesar).

Funcțiia de bază a OpenGL este de a accepta primitive, cum ar fi puncte, linii și poligoane, și de a le converti în pixeli. Acest lucru se face printr-o conductă grafică (graphics pipeline), cunoscută sub numele de mașină de stare OpenGL. Cele mai multe comenzi OpenGL primitive, sunt fie probleme la conducta grafică, sau configurarea felului în care aceste procese de conducte de primitive. Înainte de introducerea OpenGL 2.0, fiecare etapă din conductă efectua o funcție fixă și a fost configurabilă numai în limite restrânse. OpenGL 2.0 oferă mai multe etape, care sunt pe deplin programabile folosind GLSL.

OpenGL este un API procedural de nivel mic, care necesită ca un programator să impună măsurile exacte necesare pentru a face o scenă. Acest lucru contrastează cu alte API-uri, în care un programator are nevoie doar pentru a descrie o scenă și poate lăsa biblioteca să gestioneze detalile redând finalul scenei. OpenGL's de nivel mic, impune programatorilor să aibă o bună cunoaștere a conductei grafice, dar, de asemenea, oferă o anumită libertatea de a pune în aplicare algoritmi noi de redare.

OpenGL are un istoric de influențe de la dezvoltarea acceleratoarelor 3D, promovând un nivel de bază de funcționalitate, care este acum în comun cu nivelul hardware-ului de consum:

Exemple

Acest exemplu va elabora un pătrat verde de pe ecran. OpenGL are mai multe moduri de a realiza această sarcină, dar acest lucru este cel mai ușor de înțeles. Cu toate acestea, cititorul ar trebui să fie conștient de faptul că cea mai mare parte din API-urile folosite în codul de mai jos au fost scoase din uz în și după specificațiile OpenGL 3.0.

glClear( GL_COLOR_BUFFER_BIT );

Această declarație golește tamponul de culoare, astfel încât ecranul va începe gol.

glMatrixMode( GL_PROJECTION ); /* Subsequent matrix commands will affect the projection matrix */
glLoadIdentity(); /* Initialise the projection matrix to identity */
glFrustum( -1, 1, -1, 1, 1, 1000 ); /* Apply a perspective-projection matrix */

Aceste declarații vor inițializa matricea de proiecție, stabilind o matrice 3D care reprezintă zona de vizualizat. Această matrice transformă obiecte de la aparatul de fotografiat din spațiu relativ la spațiul de proiecție al OpenGL.

glMatrixMode( GL_MODELVIEW ); /* Subsequent matrix commands will affect the modelview matrix */
glLoadIdentity(); /* Initialise the modelview to identity */
glTranslatef( 0, 0, -3 ); /* Translate the modelview 3 units along the Z axis */

Aceste declarații inițializează matricea modelview. Această matrice definește o transformare de la model de-relativă coordonate în spațiu la aparat de fotografiat. Combinația matricei modelview și matricea de proiecție transformă obiectele de la modelul spațiu de proiecție comparativ cu spațiul ecranului.

glBegin( GL_POLYGON ); /* Begin issuing a polygon */
glColor3f( 0, 1, 0 ); /* Set the current color to green */
glVertex3f( -1, -1, 0 ); /* Issue a vertex */
glVertex3f( -1, 1, 0 ); /* Issue a vertex */
glVertex3f( 1, 1, 0 ); /* Issue a vertex */
glVertex3f( 1, -1, 0 ); /* Issue a vertex */
glEnd(); /* Finish issuing the polygon */

Aceste comenzi vor desena un pătrat verde în planul XY.

OpenGL Sphere

Download: sphere.zip, sphereShader.zip, icosphere.zip, icosphereShader.zip

This page describes how to generate various spherical geometries using C++ and how to draw them with OpenGL.

Sphere

The definition of sphere is a 3D closed surface where every point on the sphere is same distance (radius) from a given point. The equation of a sphere at the origin is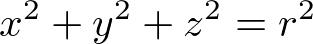

Since we cannot draw all the points on a sphere, we only sample a limited amount of points by dividing the sphere by sectors (longitude) and stacks (latitude). Then connect these sampled points together to form surfaces of the sphere.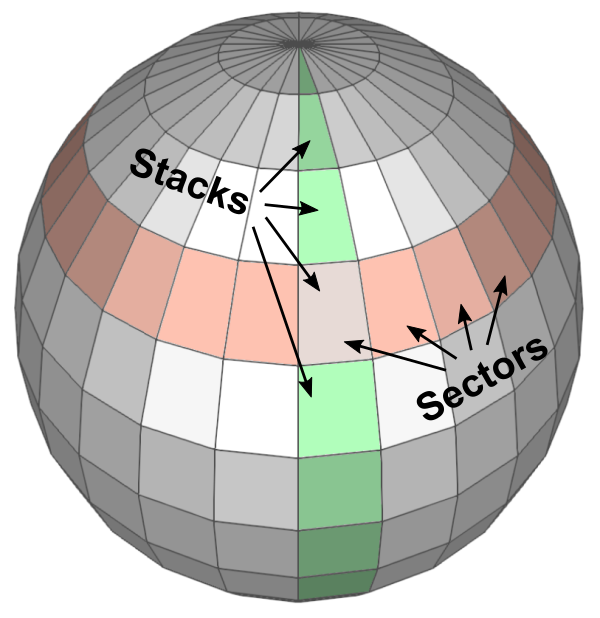

Sectors and stacks of a sphere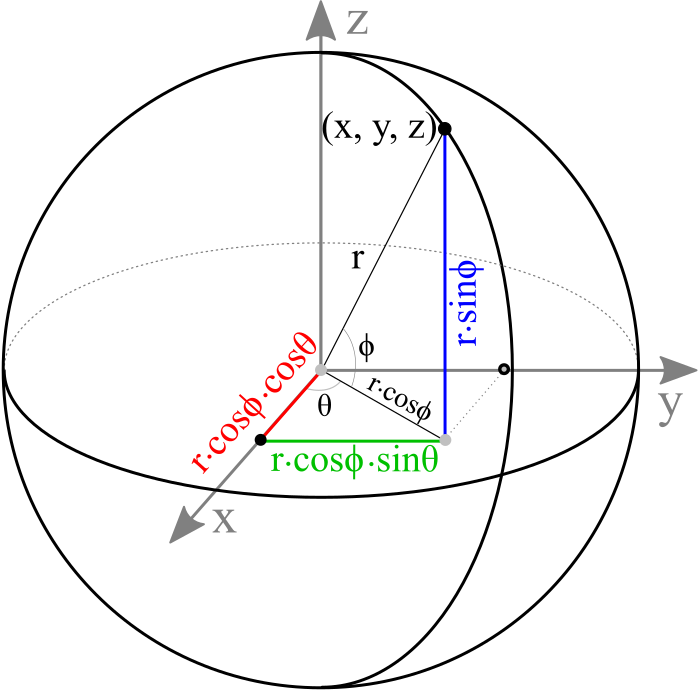

A point on a sphere using sector and stack angles

An arbitrary point (x, y, z) on a sphere can be computed by parametric equations with the corresponding sector angle θ and stack angle ϕ.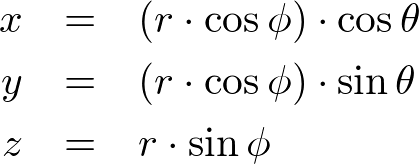

The range of sector angles is from 0 to 360 degrees, and the stack angles are from 90 (top) to -90 degrees (bottom). The sector and stack angle for each step can be calculated by the following;

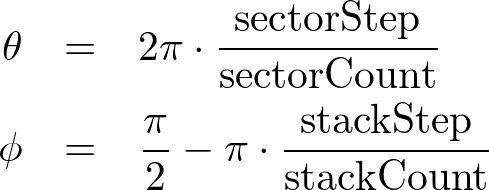The following C++ code generates all vertices of the sphere for the given radius, sectors and stacks. It also creates other vertex attributes; surface normals and texture coordinates. For more details, please refer to buildVerticesSmooth() or buildVerticesFlat() functions in Sphere.cpp class.


// clear memory of prev arrays
std::vector<float>().swap(vertices);
std::vector<float>().swap(normals);
std::vector<float>().swap(texCoords);

float x, y, z, xy;                              // vertex position
float nx, ny, nz, lengthInv = 1.0f / radius;    // vertex normal
float s, t;                                     // vertex texCoord

float sectorStep = 2 * PI / sectorCount;
float stackStep = PI / stackCount;
float sectorAngle, stackAngle;

for(int i = 0; i <= stackCount; ++i)
{
    stackAngle = PI / 2 - i * stackStep;        // starting from pi/2 to -pi/2
    xy = radius * cosf(stackAngle);             // r * cos(u)
    z = radius * sinf(stackAngle);              // r * sin(u)

    // add (sectorCount+1) vertices per stack
    // the first and last vertices have same position and normal, but different tex coords
    for(int j = 0; j <= sectorCount; ++j)
    {
        sectorAngle = j * sectorStep;           // starting from 0 to 2pi

        // vertex position (x, y, z)
        x = xy * cosf(sectorAngle);             // r * cos(u) * cos(v)
        y = xy * sinf(sectorAngle);             // r * cos(u) * sin(v)
        vertices.push_back(x);
        vertices.push_back(y);
        vertices.push_back(z);

        // normalized vertex normal (nx, ny, nz)
        nx = x * lengthInv;
        ny = y * lengthInv;
        nz = z * lengthInv;
        normals.push_back(nx);
        normals.push_back(ny);
        normals.push_back(nz);

        // vertex tex coord (s, t) range between [0, 1]
        s = (float)j / sectorCount;
        t = (float)i / stackCount;
        texCoords.push_back(s);
        texCoords.push_back(t);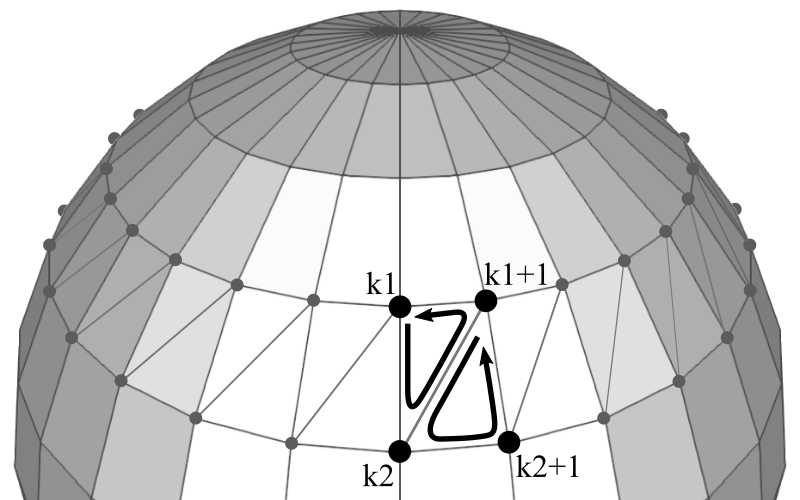
    }
}

vertex indices to draw triangles of a sphere

In order to draw the surface of a sphere in OpenGL, you must triangulate adjacent vertices to form polygons. It is possible to use a single triangle strip to render the whole sphere. However, if the shared vertices have different normals or texture coordinates, then a single triangle strip cannot be used.

Each sector in a stack requires 2 triangles. If the first vertex index in the current stack is k1 and the next stack is k2, then the counterclockwise orders of vertex indices of 2 triangles are;
k1 ⟶ k2 ⟶ k1+1
k1+1 ⟶ k2 ⟶ k2+1

But, the top and bottom stacks require only one triangle per sector. The code snippet to generate all triangles of a sphere may look like;


// generate CCW index list of sphere triangles
std::vector<int> indices;
int k1, k2;
for(int i = 0; i < stackCount; ++i)
{
    k1 = i * (sectorCount + 1);     // beginning of current stack
    k2 = k1 + sectorCount + 1;      // beginning of next stack

    for(int j = 0; j < sectorCount; ++j, ++k1, ++k2)
    {
        // 2 triangles per sector excluding first and last stacks
        // k1 => k2 => k1+1
        if(i != 0)
        {
            indices.push_back(k1);
            indices.push_back(k2);
            indices.push_back(k1 + 1);
        }

        // k1+1 => k2 => k2+1
        if(i != (stackCount-1))
        {
            indices.push_back(k1 + 1);
            indices.push_back(k2);
            indices.push_back(k2 + 1);
        }
    }
}

Example: Sphere

Download: sphere.zip, sphereShader.zip (Updated: 2018-12-13)

This example constructs spheres with 36 sectors and 18 stacks, but with different shadings; flat, smooth or textured. Sphere.cpp class provides pre-defined functions; draw(), drawWithLines() and drawLines(), to draw a sphere using OpenGL VertexArray.


// create a sphere with radius=1, sectors=36, stacks=18, smooth=true (default)
Sphere sphere(1.0f, 36, 18);

// can change parameters later
sphere.setRadius(2.0f);
sphere.setSectorCount(72);
sphere.setStackCount(24);
sphere.setSmooth(false);
...

// draw sphere using vertexarray
sphere.draw();

This C++ class also provides getVertices(), getIndices(), getInterleavedVertices(), etc. in order to access the vertex data in GLSL. The following code draws a sphere with interleaved vertex data using VBO and GLSL. Or, download sphereShader.zip for more details.


// create a sphere with default params; radius=1, sectors=36, stacks=18, smooth=true
Sphere sphere;

// copy interleaved vertex data (V/N/T) to VBO
GLuint vboId;
glGenBuffers(1, &vboId);
glBindBuffer(GL_ARRAY_BUFFER, vboId);           // for vertex data
glBufferData(GL_ARRAY_BUFFER,                   // target
             sphere.getInterleavedVertexSize(), // data size, # of bytes
             sphere.getInterleavedVertices(),   // ptr to vertex data
             GL_STATIC_DRAW);                   // usage

// copy index data to VBO
GLuint iboId;
glGenBuffers(1, &iboId);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, iboId);   // for index data
glBufferData(GL_ELEMENT_ARRAY_BUFFER,           // target
             sphere.getIndexSize(),             // data size, # of bytes
             sphere.getIndices(),               // ptr to index data
             GL_STATIC_DRAW);                   // usage
...


// bind VBOs
glBindBuffer(GL_ARRAY_BUFFER, vboId);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, iboId);

// activate attrib arrays
glEnableVertexAttribArray(attribVertex);
glEnableVertexAttribArray(attribNormal);
glEnableVertexAttribArray(attribTexCoord);

// set attrib arrays with stride and offset
int stride = sphere.getInterleavedStride();     // should be 32 bytes
glVertexAttribPointer(attribVertex,   3, GL_FLOAT, false, stride, (void*)0);
glVertexAttribPointer(attribNormal,   3, GL_FLOAT, false, stride, (void*)(sizeof(float)*3));
glVertexAttribPointer(attribTexCoord, 2, GL_FLOAT, false, stride, (void*)(sizeof(float)*6));

// draw a sphere with VBO
glDrawElements(GL_TRIANGLES,                    // primitive type
               sphere.getIndexCount(),          // # of indices
               GL_UNSIGNED_INT,                 // data type
               (void*)0);                       // offset to indices

// deactivate attrib arrays
glDisableVertexAttribArray(attribVertex);
glDisableVertexAttribArray(attribNormal);
glDisableVertexAttribArray(attribTexCoord);

// unbind VBOs
glBindBuffer(GL_ARRAY_BUFFER, 0);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, 0);

Since this C++ class uses cylindrical texture mapping, there is a squeeze/distortion at the north and south pole area. This problem can be solved using Icosphere.

Icosphere / Geosphere

Another way to create a spherical geometry is subdividing an icosahedron multiple times. Icosahedron is a regular polyhedron with 12 vertices and 20 equilateral triangles (the first left image below). Each triangle of an icosahedron is divided into 4 equal sub-triangles per subdivision.

Icosphere at subdivision 0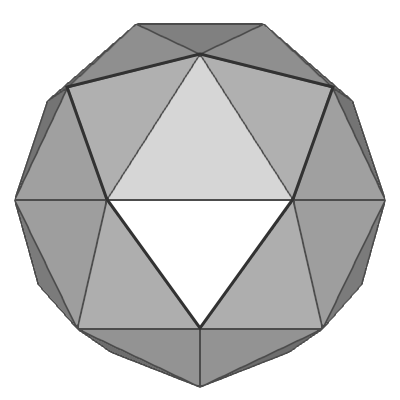

Icosphere at subdivision 1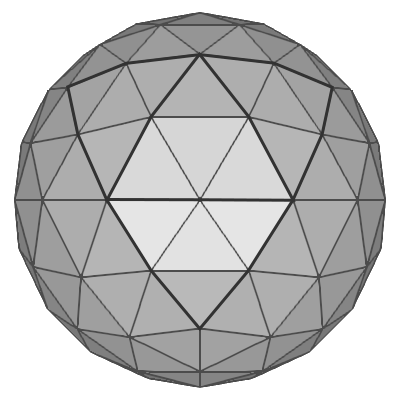

Icosphere at subdivision 2

Icosphere at subdivision 3

One way to construct 12 vertices of an icosahedron is using spherical coordinates; aligning 2 vertices at the north and south poles, and the other 10 vertices are placed at latitude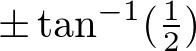

degrees and 72° aside on the same latitude. Please see the following orthogonal projection images of icosahedron.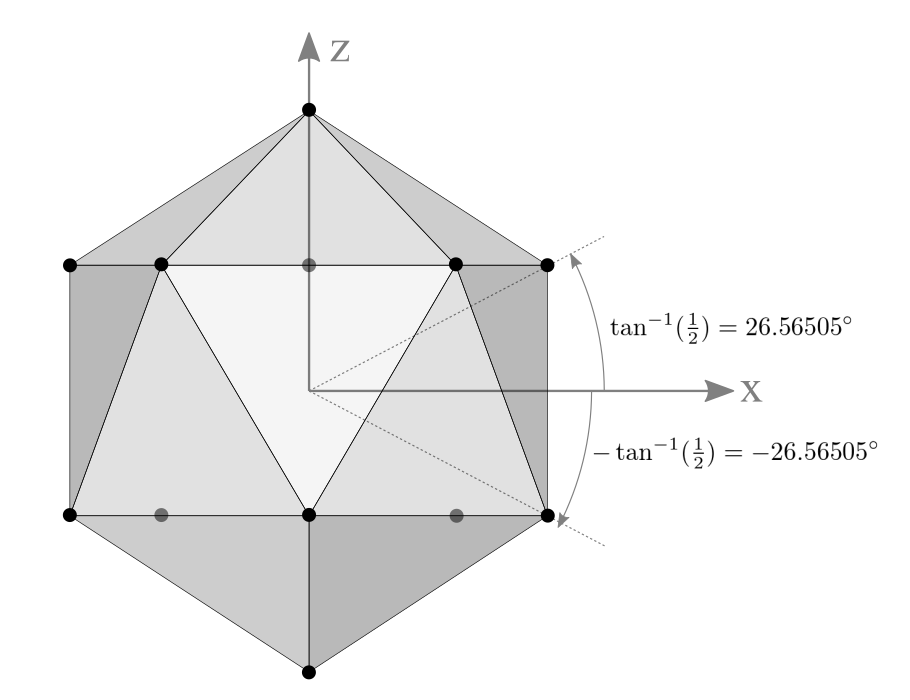

Side View of Icosahedron
2 vertices are at north/south pole and 10 vertices are at elevation ±26.565°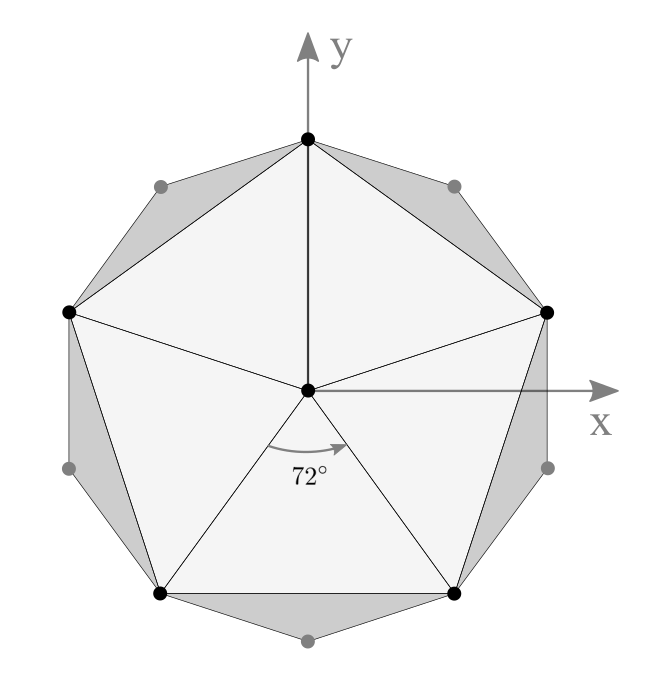

Top View of Icosahedron
5 vertices are 72° apart at the same elevation

A typical point at latitude 26.565° and radius r can be computed by;

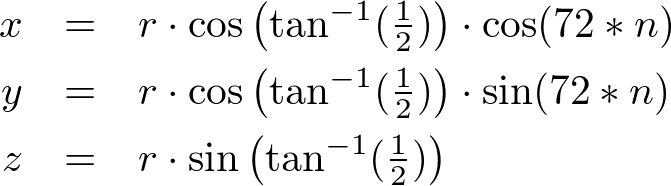Note that

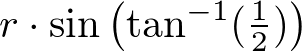is the elevation (height) of the point and

is the length of the projected line segment on XY plane.

The following C++ code is to generate 12 vertices of an icosahedron for a given radius, or you can find the complete implementation of Icosahedron.cpp or Icosphere.cpp class.


// constants
const float PI = 3.1415926f;
const float H_ANGLE = PI / 180 * 72;    // 72 degree = 360 / 5
const float V_ANGLE = atanf(1.0f / 2);  // elevation = 26.565 degree

std::vector<float> vertices(12 * 3);    // array of 12 vertices (x,y,z)
int i1, i2;                             // indices
float z, xy;                            // coords
float hAngle1 = -PI / 2 - H_ANGLE / 2;  // start from -126 deg at 1st row
float hAngle2 = -PI / 2;                // start from -90 deg at 2nd row

// the first top vertex at (0, 0, r)
vertices[0] = 0;
vertices[1] = 0;
vertices[2] = radius;

// compute 10 vertices at 1st and 2nd rows
for(int i = 1; i <= 5; ++i)
{
    i1 = i * 3;         // index for 1st row
    i2 = (i + 5) * 3;   // index for 2nd row

    z  = radius * sinf(V_ANGLE);            // elevaton
    xy = radius * cosf(V_ANGLE);            // length on XY plane

    vertices[i1] = xy * cosf(hAngle1);      // x
    vertices[i2] = xy * cosf(hAngle2);
    vertices[i1 + 1] = xy * sinf(hAngle1);  // y
    vertices[i2 + 1] = xy * sinf(hAngle2);
    vertices[i1 + 2] = z;                   // z
    vertices[i2 + 2] = -z;

    // next horizontal angles
    hAngle1 += H_ANGLE;
    hAngle2 += H_ANGLE;
}

// the last bottom vertex at (0, 0, -r)
i1 = 11 * 3;
vertices[i1] = 0;
vertices[i1 + 1] = 0;
vertices[i1 + 2] = -radius;

The subdivision algorithm is splitting the 3 edge lines of each triangle in half, then extruding the new middle point outward, so its length (the distance from the center) is the same as sphere's radius.


std::vector<float> tmpVertices;
std::vector<float> tmpIndices;
const float *v1, *v2, *v3;          // ptr to original vertices of a triangle
float newV1[3], newV2[3], newV3[3]; // new vertex positions
unsigned int index;

// iterate all subdivision levels
for(int i = 1; i <= subdivision; ++i)
{
    // copy prev vertex/index arrays and clear
    tmpVertices = vertices;
    tmpIndices = indices;
    vertices.clear();
    indices.clear();
    index = 0;

    // perform subdivision for each triangle
    for(int j = 0; j < tmpIndices.size(); j += 3)
    {
        // get 3 vertices of a triangle
        v1 = &tmpVertices[tmpIndices[j] * 3];
        v2 = &tmpVertices[tmpIndices[j + 1] * 3];
        v3 = &tmpVertices[tmpIndices[j + 2] * 3];

        // compute 3 new vertices by spliting half on each edge
        //         v1       
        //        / \       
        // newV1 *---* newV3
        //      / \ / \     
        //    v2---*---v3   
        //       newV2      
        computeHalfVertex(v1, v2, newV1);
        computeHalfVertex(v2, v3, newV2);
        computeHalfVertex(v1, v3, newV3);

        // add 4 new triangles to vertex array
        addVertices(v1,    newV1, newV3);
        addVertices(newV1, v2,    newV2);
        addVertices(newV1, newV2, newV3);
        addVertices(newV3, newV2, v3);

        // add indices of 4 new triangles
        addIndices(index,   index+1, index+2);
        addIndices(index+3, index+4, index+5);
        addIndices(index+6, index+7, index+8);
        addIndices(index+9, index+10,index+11);
        index += 12;    // next index
    }
}


///////////////////////////////////////////////////////////////////////////////
// find middle point of 2 vertices
// NOTE: new vertex must be resized, so the length is equal to the radius
///////////////////////////////////////////////////////////////////////////////
void computeHalfVertex(const float v1[3], const float v2[3], float newV[3])
{
    newV[0] = v1[0] + v2[0];    // x
    newV[1] = v1[1] + v2[1];    // y
    newV[2] = v1[2] + v2[2];    // z
    float scale = radius / sqrtf(newV[0]*newV[0] + newV[1]*newV[1] + newV[2]*newV[2]);
    newV[0] *= scale;
    newV[1] *= scale;
    newV[2] *= scale;
}

In order to generate a texture map of an icosphere, you need to unwrap the 3D geometry on a plane (paper model). I use the following texture coordinates of vertices instead of normalized coordinates from 0 to 1, so the coordinate of each vertex can be snapped to an exact pixel on the image. For example, if a texture size is 2048x1024, then the horizontal step is 186 pixels and the vertical step is 322 pixels.

Texture coordinates of Icosphere, where S=186/2048, T=322/1024

Example: Icosphere

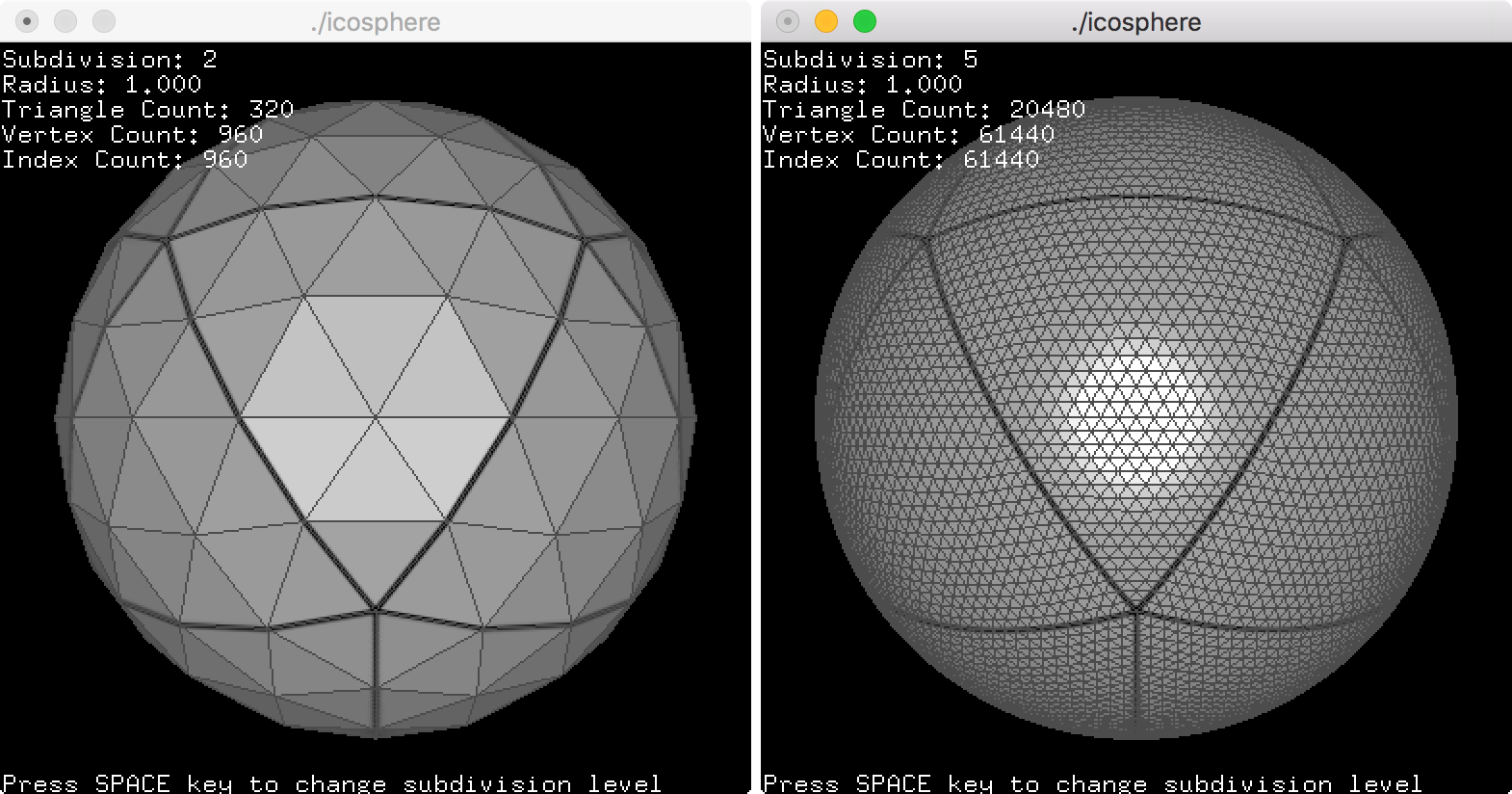
This example is to draw an icosphere with a texture. Press the spacebar key to change the subdivision level. If the subdivision is 2, the icosphere consists of 320 triangles, and if the subdivision is 5, it has 20,480 triangles.
Download: icosphere.zip, icosphereShader.zip, icosahedron.zip

Drawing an icosphere in OpenGL is identical to Sphere C++ class object. Please refer to Sphere examplesection above. To construct an icosphere object, it requires 3 parameters; radius, subdivision and surface smoothness. You can change the radius and subdivision level after it has been constructed. If the subdivision is 0, then it is the same as an icosahedron.


// create icosphere with radius=1, subdivision=5 and smooth shading=true
Icosphere sphere(1.0f, 5, true);

// can change parameters later
sphere.setRadius(2.0f);
sphere.setSubdivision(6);
sphere.setSmooth(false);
...

// draw icosphere using vertexarray
sphere.draw();
...

// copy interleaved vertex data (V/N/T) to VBO
GLuint vboId;
glGenBuffers(1, &vboId);
glBindBuffer(GL_ARRAY_BUFFER, vboId);           // for vertex data
glBufferData(GL_ARRAY_BUFFER,                   // target
             sphere.getInterleavedVertexSize(), // data size, # of bytes
             sphere.getInterleavedVertices(),   // ptr to vertex data
             GL_STATIC_DRAW);                   // usage

// copy index data to VBO
GLuint iboId;
glGenBuffers(1, &iboId);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, iboId);   // for index data
glBufferData(GL_ELEMENT_ARRAY_BUFFER,           // target
             sphere.getIndexSize(),             // data size, # of bytes
             sphere.getIndices(),               // ptr to index data
             GL_STATIC_DRAW);                   // usage
...

// draw icosphere using VBO and GLSL
int stride = sphere.getInterleavedStride();     // should be 32 bytes
glVertexAttribPointer(attribVertex,   3, GL_FLOAT, false, stride, (void*)0);
glVertexAttribPointer(attribNormal,   3, GL_FLOAT, false, stride, (void*)(sizeof(float)*3));
glVertexAttribPointer(attribTexCoord, 2, GL_FLOAT, false, stride, (void*)(sizeof(float)*6));
glDrawElements(GL_TRIANGLES,
               sphere.getIndexCount(),
               GL_UNSIGNED_INT,
               (void*)0);
...

http://www.songho.ca/opengl/gl_sphere.html

Algoritmi paraleli

Friday, July 12, 2019

OpenGL

Functii grafice în mediul OpenGL

https://www3.ntu.edu.sg/home/ehchua/programming/opengl/CG_Introduction.html

TUTORIAL

Implementări

Design

Exemple

OpenGL Sphere

Sphere

Example: Sphere

Icosphere / Geosphere

Example: Icosphere

No comments:

Post a Comment

Blog Archive

GL_POINT_SMOOTH	Daca este activata, functia confera unui punct un aspect neted,altfel marginile acestuia vor fi bine definite (engl. aliased)
GL_LINE_SMOOTH	Similar pentru o linie
GL_LINE_STIPPLE	Daca este activata, functia foloseste aspectul predefinit pentru o linie.