APD - o materie foarte interesanta, dar avand in vedere ca se face cu Nasu' cursul este foarte, foarte plictisitor. Se predau o gramada de algoritmi, mai intai paraleli (ca idee pentru mai multe procesoare in acelasi sistem sau pentru multithreading), apoi distribuiti (pentru mai multe sisteme care ruleaza acelasi program, in principiu). Sunt cativa algoritmi clasici, cei distribuiti sunt baza pentru examen (alegerea liderului, stabilirea topologiei, algoritmi unda- daca stii astea sigur treci), plus inca 2-3 exemple simple la algoritmi paraleli, gen cautare paralela, mutexuri, problema cititorilor si scriitorilor.
In principiu materia e foarte putina comparativ cu PC, sunt doar cativa algoritmi de invatat. La examen se corecteaza mult, mult mai lejer.
Punctajul e ca la PC
- 4 puncte pe teme,
- 1 punct pe lab,
- 1.5 puncte pe teste la lab si la curs,
- 6.5 puncte trunchiate la 6.
Laboratorul este decent, desi la inceput o sa para destul de complicat. Temele au fost foarte simple, 2 din ele, a fost una mai naspa in java, asistentul si-a facut testele foarte dubios si a trebuit sa ii explic pe forum ca nu merge cum ar trebui (era o parsare pe niste texte si nu isi definise bine delimitatorii.. o gramada de probleme de aici), dar ideea temei nu era grea, pacat ca au fost teste tampite. Ultimele 2 teme se gaseau pe net, a 3-a oricum era foarte simpla si nu avea sens sa o copiezi, iar a 4-a nu era chiar la fel, dar te puteai inspira. Oricum, temele au fost decente.
La examen au picat destul de putini, corectarea a fost lejera.
Cum treci:
- mergi la lab,
- faci 2 teme (alea usoare) sau macar o tema cu punctaj mare pe testele de curs.
La examen ar trebui sa stii in mare fiecare algoritm pentru ca da din orice, inclusiv din ce te astepti mai putin, in afara de algoritmi genetici nu e nimic care sa nu se poata da.
Cum iei 10: mai simplu ca la PC, in orice caz, faci temele, vii la lab si inveti bine algoritmii aia pentru examen, oricum da doar din ei.
APD (Algoritmi Paraleli si Distribuiti)
Curs: Elena Apostol
Laborator: Radu-Ioan Ciobanu
Laborator: Radu-Ioan Ciobanu
Trupa de la PC, inca un semestru; de data asta prezentand tot felul de algoritmi pt calcul paralel (multithreaded) si distribuit (pe diverse statii/cluster).
Curs: interesant pana la un punct; acopera ceva despre openMP (care se rezuma cam la o singura instructiune) paralelism in Java si mesaje cu openMPI. Plus o groaza de algoritmi scrisi intr-un pseudocod ceva mai bizar, care se vor cere la examen + complexitati. Din ce am auzit, cursul seamana surprinzator de mult cu cel de la seria CC (adica pdf-urile erau aceleasi...). Parerea proprie si personala: se putea aloca mai mult timp si imbunatati tehnica de predare :/
Testele de prezenta sunt destul de dificile uneori.
Laboratorul: am nimerit bine; explicatii bune, punctaj ok, asistent super. Cealalta semigrupa a facut cu o persoana... a very special snowflake :)), acelasi care a scris si exercitiile pt laburi. Seamana cu laboratorul de PA ca nivel de dificultate - insa aici erau ceva mai multe probleme si se foloseau algoritmi care nu erau in curs. Because why not? Urat de debuggat si mult de scris - beware.
Teme: 3. La prima de scris un algoritm si paralelizat cu openMP (aka bagi #pragma omp for peste tot si vezi daca merge), a 2-a in Java si destul de comoda. A 3-a a fost mai lunga: un program care sa ia niste poze, pe urma sa stabileasca un arbore de acoperire pt retea si sa trimita bucati din poza pt procesare (aplicat blur, sharpen, etc.) la fiecare sistem iar la final sa primeasca bucatile inapoi si sa construiasca poza modificata.
La examen: structura de la PC - dat pe numere, 1 subiect de 2 puncte, 1 de un punct si 2 la alegere (fiecare de 1 punct, se puncteaza un singur subiect). De obicei primul exercitiu face diferenta intre trecut si picat...problema apare cand primul subiect iti cere sa scrii un algoritm de 2-3 pagini (problema terminarii), care in curs e prezentat cu 4 idei pe jumatate de slide...Nu-s prea echilibrate foile de examen dar se corecteaza ok...sa zicem. Se cam vedea dupa nota cine si ce numar a avut...
Bibliografie extra
https://ftp.utcluj.ro/pub/users/civan/CPD/1_RESURSE/Open_Book_2010_buildingPP_Kaminsky.pdf
https://ftp.utcluj.ro/pub/users/civan/CPD/1_RESURSE/Open_Book_2014_ParProcBook_Mathloff.pdf
http://web.stanford.edu/~jlmcc/papers/PDP/Volume%201/Chap1_Part1_PDP86.pdf
Definitie: doua operatii se pot executa in paralel daca sunt independente. Calculul seriei Fibonacci folosind formula: F(n) = F(n-1) + F(n-2) nu poate fi făcut folosind un algoritm paralel deoarece fiecare termen depinde de cel anterior.
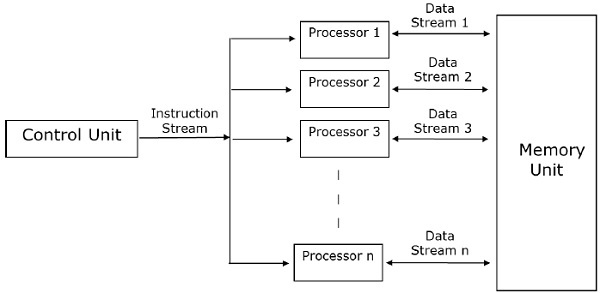
What is Parallel Computing?
 Serial Computing:
Serial Computing:- Traditionally, software has been written for serial computation:
- A problem is broken into a discrete series of instructions
- Instructions are executed sequentially one after another
- Executed on a single processor
- Only one instruction may execute at any moment in time

For example:

 Parallel Computing:
Parallel Computing:- In the simplest sense, parallel computing is the simultaneous use of multiple compute resources to solve a computational problem:
- A problem is broken into discrete parts that can be solved concurrently
- Each part is further broken down to a series of instructions
- Instructions from each part execute simultaneously on different processors
- An overall control/coordination mechanism is employed

For example:

- The computational problem should be able to:
- Be broken apart into discrete pieces of work that can be solved simultaneously;
- Execute multiple program instructions at any moment in time;
- Be solved in less time with multiple compute resources than with a single compute resource.
- The compute resources are typically:
- A single computer with multiple processors/cores
- An arbitrary number of such computers connected by a network
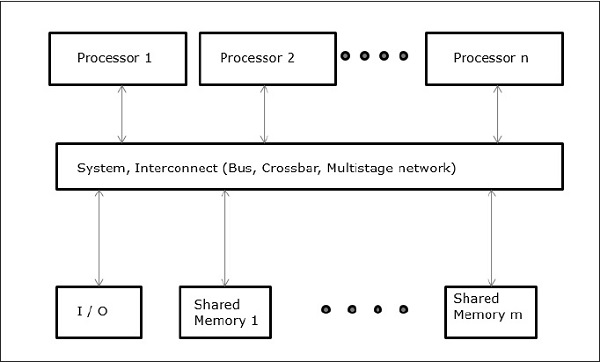
 Parallel Computers:
Parallel Computers:- Virtually all stand-alone computers today are parallel from a hardware perspective:
- Multiple functional units (L1 cache, L2 cache, branch, prefetch, decode, floating-point, graphics processing (GPU), integer, etc.)
- Multiple execution units/cores
- Multiple hardware threads

IBM BG/Q Compute Chip with 18 cores (PU) and 16 L2 Cache units (L2) - Networks connect multiple stand-alone computers (nodes) to make larger parallel computer clusters.

- For example, the schematic below shows a typical LLNL parallel computer cluster:
- Each compute node is a multi-processor parallel computer in itself
- Multiple compute nodes are networked together with an Infiniband network
- Special purpose nodes, also multi-processor, are used for other purposes

- The majority of the world's large parallel computers (supercomputers) are clusters of hardware produced by a handful of (mostly) well known vendors.

Source: Top500.org
https://pdfs.semanticscholar.org/09ed/7308fdfb0b640077328aa4fd10ce429f511a.pdf?_ga=2.236562818.262307220.1561817530-644819069.1561817530
GPRM : a high performance programming framework for manycore processors - teza de doctorat
- Published 2016
Processors with large numbers of cores are becoming commonplace. In order to utilise the available resources in such systems, the programming paradigm has to move towards increased parallelism. However, increased parallelism does not necessarily lead to better performance. Parallel programming models have to provide not only flexible ways of defining parallel tasks, but also efficient methods to manage the created tasks. Moreover, in a generalpurpose system, applications residing in the system compete for the shared resources. Thread and task scheduling in such a multiprogrammed multithreaded environment is a significant challenge. In this thesis, we introduce a new task-based parallel reduction model, called the Glasgow Parallel Reduction Machine (GPRM). Our main objective is to provide high performance while maintaining ease of programming. GPRM supports native parallelism; it provides a modular way of expressing parallel tasks and the communication patterns between them. Compiling a GPRM program results in an Intermediate Representation (IR) containing useful information about tasks, their dependencies, as well as the initial mapping information. This compile-time information helps reduce the overhead of runtime task scheduling and is key to high performance. Generally speaking, the granularity and the number of tasks are major factors in achieving high performance. These factors are even more important in the case of GPRM, as it is highly dependent on tasks, rather than threads. We use three basic benchmarks to provide a detailed comparison of GPRM with Intel OpenMP, Cilk Plus, and Threading Building Blocks (TBB) on the Intel Xeon Phi, and with GNU OpenMP on the Tilera TILEPro64. GPRM shows superior performance in almost all cases, only by controlling the number of tasks. GPRM also provides a low-overhead mechanism, called “Global Sharing”, which improves performance in multiprogramming situations. We use OpenMP, as the most popular model for shared-memory parallel programming as the main GPRM competitor for solving three well-known problems on both platforms: LU factorisation of Sparse Matrices, Image Convolution, and Linked List Processing. We focus on proposing solutions that best fit into the GPRM’s model of execution. GPRM outperforms OpenMP in all cases on the TILEPro64. On the Xeon Phi, our solution for the LU Factorisation results in notable performance improvement for sparse matrices with large numbers of small blocks. We investigate the overhead of GPRM’s task creation and distribution for very short computations using the Image Convolution benchmark. We show that this overhead can be mitigated by combining smaller tasks into larger ones. As a result, GPRM can outperform OpenMP for convolving large 2D matrices on the Xeon Phi. Finally, we demonstrate that our parallel worksharing construct provides an efficient solution for Linked List processing and performs better than OpenMP implementations on the Xeon Phi. The results are very promising, as they verify that our parallel programming framework for manycore processors is flexible and scalable, and can provide high performance without sacrificing productivity.
În programare un algoritm de calcul paralel sau concurent, în opoziție cu unul secvențial, este un algoritm care poate fi executat (simultan) pe porțiuni pe mai multe mașini de calcul, apoi reasamblat pentru aflarea rezultatului final. Algoritmii de calcul paralel sunt importanți datorită îmbunătățirilor aduse sistemelor de calcul multiprocesor. În general e mai ușor să construiești un singur microprocesor rapid decât o serie de microprocesoare lente care îndeplinesc aceeași funcție. În prezent creșterea vitezei unui singur procesor nu mai este posibilă atingăndu-se pragul superior în ceea ce privește mărimea și temperatura de funcționare. Atingerea acestui prag face practică implementarea de sisteme multiprocesor și pe sistemele de dimensiuni reduse cum ar fi calculatoarele personale. Cuprins
1 Motivație
2 Problematica programării paralele
2.1 Exemple de aplicații
3 Proiectarea unui algoritm paralel
3.1 Problema comunicației
3.2 Partiționarea problemei
3.3 Alocarea
4 Limitele programării paralele
4.1 Factorii ce afectează performanța algoritmilor paraleli[2]
Conceptul de paralelism a fost investigat în ultimele trei decenii. În trecut, calculul paralel rămăsese la nivel de concept, deoarece costurile inițiale legate de implementare erau ridicate. Din aceste cauze nu era practică investitia inițială într-un sistem de calcul paralel. În ultimii ani o dată cu scaderea costurilor tehnologiei au apărut o multitudine de mașini de calcul care pot reduce timpul de rezolvare al problemelor prin implementarea unor algoritmi de calcul paralel. Problematica programării paralele Orice rezolvare de problemă prin programare paralelă, necesită în prealabil determinarea necesității adoptării unei soluții paralele, deoarece pot exista soluții de rezolvare secvențiale mai eficiente. Un exemplu de problemă de calcul paralel ar fi simularea unui cutremur și determinarea punctului cel mai afectat de acesta. Următorii pași presupun: Identificarea părților paralelizabile ale programului Identificarea botellneck-urilor Identificarea potențialilor inhibitori ai paralelismului. Un exemplu de astfel de inhibitor ar fi acela de dependență al datelor, așa cum am demonstrat în problema seriei lui Fibonacci Investigarea cât mai multor algoritmi de calcul paralel, unele soluții fiind mai eficiente decât altele. Exemple de aplicații Modelare și simulare: prognoza meteo, dinamica moleculară Inteligența artificială: rețele neuronale Grafica: Multimedia, realitate virtuală, cinematografie Motoare de căutare Proiectarea unui algoritm paralel Una dintre cele mai importante trăsături ale unui algoritm paralel este divizarea problemei în subprobleme care pot fi distribuite pe mai multe taskuri. Pentru proiectarea unui algoritm paralel se pot considera o serie de abordări. Prima ar fi paralelizarea unui algoritm secvențial deja existent. Pentru aceasta va trebui să se determine paralelismul care apare în mod natural în cadrul unui algoritm secvențial . Uneori, se preferă găsirea unei soluții diferite de cea oferită de algoritmul secvențial ceea ce presupune o regândire a întregului algoritm. Indiferent de modul de abordare în cadrul unui algoritm paralel nu se pot ignora o serie de considerații importante. Una din acestea este costul de comunicație între procese. Dacă la un algoritm secvențial costul sau complexitatea este exprimată în spațiu (mărimea memoriei ocupate) și timp (numărul de cicli de ceas) necesar pentru a executa un program, la cel paralel trebuie luat în considerare și modul în care se comunică între procese. Problema comunicației Există unii algoritmi de calcul paralel care nu au nevoie de comunicare între procese. Spre exemplu dacă ne imaginăm un algoritm paralel care face conversia unei imagini color în una alb negru. Datele din acea imagine pot fi distribuite pe mai multe taskuri independente. Acest tip de probleme sunt denumite "embarrassingly parallel" [1] (paralelism jenant) deoarece comunicarea ]între taskuri este foarte redusă. Cei mai mulți algoritmi paraleli sunt algoritmi complecși în care comunicația între procese are o importanță majoră. Complexitatea algoritmilor paraleli este calculată în funcție de memoria folosită și timp. Ei trebuie să mai optimizeze folosirea unei alte resurse, comunicarea între procese/procesoare. Sunt două modalități prin care procesele/procesoarele comunică: Memorie partajată sau Folosind mesaje. Modelul cu memorie partajată se referă la programarea într-un mediu multiprocesor pentru care comunicația între procese se realizează prin intermediul unei memorii comune. Modelul cu transfer de mesaje este adecvat implementării unui algoritm paralel într-o rețea de calculatoare. Pentru ca un program să poată fi executat în paralel acesta trebuie descompus într-o serie de procese. Aceasta descompunere presupune partiționarea algoritmului și alocarea proceselor. Partiționarea reprezintă specificarea setului de taskuri care implementează algoritmul în modul cel mai eficient pe o mașină de calcul paralel. Alocarea reprezintă modul de distribuire a task-urilor procesoarelor. Partiționarea problemei Granularitatea unui algoritm Performanța unui algoritm de calcul paralel depinde de granularitate. Aceasta se referă la mărimea task-ului în comparație cu timpul necesar comunicației și sincronizării datelor. Dacă timpul necesar comunicației și sincronizării este mai mare decât timpul de execuție al task-ului atunci granularitatea este mică. O soluție este partiționarea programului în taskuri de dimensiuni mai mari cu o granularitate grosieră. Dezavantajul acestei metode este reducerea gradului de paralelism. Îmbunătățirea performanțelor unui algoritm de calcul paralel se face prin găsirea unui compromis între mărimea task-ului și consumul suplimentar de resurse. De obicei este găsită o corelare între numărul de taskuri, dimensiunea acestora și menținerea la minimu necesar a consumului suplimentar de resurse. Cea mai bună granularitate este cea obținută prin adaptarea algoritmului pe platforma hardware pe care rulează. În majoritatea cazurilor overhead-ul asociat comunicațiilor și sincronizării este mare în comparație cu timpul de execuție caz în care se preferă o granularitate grosieră. Partiționarea unui algoritm se poate face în două moduri: Statică: Partiționarea se face înainte de execuție. Avantajul acestei metode este acela că necesită un volum redus de comunicații. Pe de altă parte metoda aceasta prezintă dezavantajul ca gradul de paralelism să fie dat de datele de intrare. Dinamică: Generarea task-urilor este făcută în timpul de execuție al programului. Avantajul acestei metode este dat de menținerea procesoarelor ocupate cu prețul creșterii volumului comunicației dintre procese. Alocarea task-urilor în funcție de disponibilitate Alocarea Alocarea reprezintă distribuirea de taskuri procesoarelor. Planificarea ca și în cazul partiționării poate fi statică sau dinamică. În cazul alocării statice sarcinile și ordinea de execuție sunt cunoscute înainte de execuție. Algoritmii de calcul paralel ce folosesc planificarea statică necesită un volum mic de comunicare între procese potrivită pentru cazurile când costurile de comunicație este mare. În cazul planificării dinamice alocarea sarcinilor este făcută la rulare. Această tehnică permite distribuirea uniformă a încărcării procesoarelor și oferă flexibilitate în utilizarea unui număr mare de procesoare. Astfel dacă un procesor termină mai repede task-ul alocat i se poate atribui un alt task mărind în acest mod eficiența algoritmului. Dezavantaje: volumul de "overhead" este mare modul de execuție este greu de urmărit analiza performanțelor devine dificilă, ca urmare a alocării task-urilor în timpul rulării. Limitele programării paralele Conform legii lui Amdahl accelerarea unui program este dată de următoarea formulă: {\displaystyle acc={\frac {1}{(1-P)}}} {\displaystyle acc={\frac {1}{(1-P)}}}, unde P reprezintă porțiunea din cod care poate fi paralelizată. Dacă nici o porțiune a programului nu poate fi paralelizată atunci accelerarea este 1 (algoritm secvențial). Daca P=1 (tot codul poate fi paralelizat), atunci accelerarea este infinită (cel puțin teoretic). Dacă luam în considerare că un algoritm paralel rulează pe mai multe procesoare obținem următoarea formulă: {\displaystyle acc={\frac {1}{{\frac {P}{N}}+{S}}}} {\displaystyle acc={\frac {1}{{\frac {P}{N}}+{S}}}}, unde P reprezintă partea din algoritm care poate fi paralelizată, N reprezintă numărul de procesoare și S partea care nu a fost paralelizată.Cu toate că un algoritm paralel are limitele sale conform celei de-a doua formule putem concluziona că aceștia sunt foarte eficienți în rezolvarea problemelor de dimensiuni mari, în care partea secvențială rămâne neschimbată.
https://ro.wikipedia.org/wiki/Algoritmi_de_calcul_paralel
Parallel Programming and Parallel Algorithms
http://www2.cs.siu.edu/~cs401/Textbook/ch7.pdf
| ||


Algoritmi numerici

https://informatica.hyperion.ro/wp-content/uploads/2017/11/ALGORITMI-PARALELI-SI-DISTRIBUITI.pdf
Etapele descrierii unui algoritm paralel.
• Identificarea partilor problemei care se pot executa in paralel
• Maparea partilor pe mai multe procesoare
• Impartirea datelor (de intrare, iesire si intermediare)
• Gestiunea accesului la datele comune mai multor procesoare
Metrici de performanta
– Timp de Executie,
- Suprasarcina,
- Accelerare,
- Eficienta,
- Cost



ALGORITMI PARALELI ȘI DISTRIBUIȚI
ÎNDRUMAR DE LABORATOR / SEMINAR
https://informatica.hyperion.ro/wp-content/uploads/2017/11/ALGORITMI-PARALELI-SI-DISTRIBUITI.pdf
LABORATORUL NR.1 Introducere în clasa Thread . Clasa Thread din pachetul java.lang: public class Thread extends Object implements Runnable
LABORATORUL NR.2 Introducere în bibliotecile OpenMP
- Structura unui program OpenMP
- Formatul unei directive
- Directiva pentru regiune paralela
- Directiva pentru partajarea lucrului
- Directiva for
- Directiva sections
- Directiva single
- Directiva parallel for
Exemple : a) adunarea a doua matrici si b) inmultirea a doua matrici
LABORATORUL NR.3 Implementare fire de execuție. Un fir de executare este un program secvențial, ce poate fi executat concurent cu alte fire
LABORATORUL NR.4 Implementare semafoare. Semaforul este un tip de date, caracterizat deci prin valorile pe care le poate lua şi operaţiile în care poate interveni. O variabilă de tip semafor (general) poate lua ca valori doar numere naturale. Dacă valorile permise pot fi numai 0 sau 1, spunem că este vorba de un semafor binar. Conceptual, unui semafor s îi este asociată o mulţime de blocare Bs, iniţial vidă.
Exemplul 1. Problema grădinilor ornamentale
LABORATORUL NR.5 Implementarea şi testare algoritm de sortare paralelă
LABORATORUL NR.6 Implementarea unor algoritmi din metodele numerice
LABORATORUL NR.7 Testarea algoritmilor paraleli
Paralalism cu Simulink din Matlab


VIDEOS
COURSERA - se apasa stanga mouse pe text si apare linkul
Parallel Programming
Basic Task Parallel Algorithms
Data-Parallelism
Data Structures for Parallel Computing
We give a glimpse of the internals of data structures for parallel computing, which helps us understand what is happening under the hood of parallel collections.
CURSURI SI LABORATOARE UPB - Automatica si Calculatoare
Algoritmi paraleli si distribuiti
Istoric
Curs University of Waterloo !!!
YouTube
Parallel and Distributed Simulation Systems
Laboratoare:
- Laborator 1 [OneNote][pdf]
- Laborator 2 [OneNote][pdf]
- Laborator 3 [OneNote][pdf]
- Laborator 4 [OneNote][pdf]
- Laborator 1 [pdf]
- Laborator 2 [pdf]
- Laborator 3 [pdf]
- Laborator 4 [pdf]
- Laborator 6 [pdf]
- Laborator 7 [pdf]
- Laborator 8 - MPI (sortare) [pdf] Sortare prin interclasare
- Rezolvare laborator 2 [rar]
- Rezolvare laborator 3 [rar]
- Rezolvare laborator 4 [rar]
- Rezolvare laborator 5 - Replicated workers [rar]
- Rezolvare laborator 6 - Parallel binary seach [rar]
- Rezolvare laborator 7 - MPI [rar]
- Rezolvare laborator 8 - MPI (sortare) [rar]
- Rezolvare laborator 9 - MPI [zip]
- Rezolvare laborator 10 - MPI [zip]
- Rezolvare laborator 12 - MPI [zip]
- Rezolvare laborator 13 - MPI [zip]
Alte materiale:
- Tema1 - Enunt si rezolvare [zip]
- Tema2 - Enunt si rezolvare [zip]
- Tema3 - Enunt si rezolvare [zip]
- Tema4 - Enunt si rezolvare [zip]
- Subiecte examen 2011 [pdf]
- Alte subiecte examen [pdf]
- Subiecte examen [txt]
SUBIECTE EXAMEN
1.Algoritmi unda
1.1 Scheme de transmisie, definitie alg unda, proprietati 0.6
1.2 Pseudocod+complexit ate+explicatii alg inel si arbore
1.3 Sa aplici pe un arbore dat de ei alg arbore 0.4
2.Problema in care trebuia sa gasesti algoritmul pentru calculul unui polinom de ordin n,
folosind n sau n+1 procesoare si cu o complexitate de O(log n)
3.La alegere
3.1 Algoritm sondaj-ecou in ambele variante cu si fara cicluri.
3.2 Algoritm cititor-scriitor:
descrierea problemei, varianta initiala in pseudocod
algoritm cu prioritizare cititori fata de scriitori
algoritm cu prioritate pentru scriitori (foar modificarile la ce anterior si justificate)
Varianta A
1.
1.Algoritmi pt. descoperirea topologiei
1.1 Descrierea generala a problemei (0.2 p)
1.2 Algoritmul pulsatiilor cu D necunoscut. Algoritmul de sondaj cu ecou. Descrierea
algoritmilor, pseudocod, complexitate (1.4 p).
1.3 Aplicarea algoritmului pulsatiilor pe un graf dat ca exemplu (0.4 p)
2. Se dadea un sistem de ecuatii:
a11 * x1 = b1
a21 * x1 + a22 * x2 = b2
....
an1 * x1 + an2 * x2 + ... + ann * xn = bn
Aveai n procese, fiecare cunostea linia ai si bi. Trebuia scris un algoritm de complexitate O(n)
care rezolva sistemul: la final, procesul i trebuia sa cunoasca xi.
3. La alegere:
3.1 Algoritmi pentru alegerea liderului: Descrierea problemei.
Algoritmul tree si Lelann-ChangRobert. (Nu mai tin minte exact)
Algoritmul tree si Lelann-ChangRobert. (Nu mai tin minte exact)
3.2 Cautarea paralela: Descrierea problemei, algoritm, complexitate.
Varianta C 09.02
1.Algoritmi unda
1.1 Scheme de transmisie, definitie alg unda, proprietati 0.6
1.2 Pseudocod+complexit ate+explicatii alg inel si arbore 1
1.3 Sa aplici pe un arbore dat de ei alg arbore 0.4
2.Problema in care trebuia sa gasesti algoritmul pentru calculul unui polinom de ordin n, folosind
n sau n+1 procesoare si cu o complexitate de O(log n)
3.La alegere
3.1 Algoritm sondaj-ecou in ambele variante cu si fara cicluri.
3.2 Algoritm cititor-scriitor: descrierea problemei, varianta initiala in pseudocod
algoritm cu prioritizare cititori fata de scriitori
algoritm cu prioritate pentru scriitori (foar modificarile la ce anterior si justificate)
1.Algoritmi unda- prezentare generala, scheme transmitere de mesaje, proprietati. 0.6 p
Algoritmul Ecou .
Algoritmul Fazelor. Prezentare,alg + complexitate 1 p
Cazul particular alg fazelor pt clici. 0.4 p
2.O problema cu fete si baieti ( nu mai tin minte exact) 1p
3.
Complexitatea algoritmilor
- Modelul Foster. Alte modele
- Other stuff...
Sau
Semafoare distribuite
- Implementarea excluderii mutuale folosind ceasuri logice ( 0.4 p) (nici acum nu stiu unde e
rezolvata)
-
Implementarea semaforului distribuit ( algoritm ) 0.6 p
Buna,
Nu mai tin minte exact subiectele (ni le-a luat), dar pe numarul meu a fost cam asa :
Varianta B:
1.
complexitatea algoritmilor paraleli
a. de cine depinde performanta , masuri ale performantei, limite inferioare
b. modele generale, , work depth, sortarea pe un vector de procesoare
c. modelul bit , complexitate .
(probabil mai erau si altele, dar nu mai stiu)
2. o problema cu replicated workers . Era o familie care trebuia sa treaca un pod, aveau o singura
lampa. Fiecare membru al familiei avea o viteza. Pe pod treceau 1 sau 2 persoane deodata. Toti
trebuiau sa treaca de pe o parte pe alta in mai putin de 30secunde. Trebuia scris un algoritm care
sa rezolve aceasta problema (pseudocodul de la curs, nu de la laborator).
3. La alegere
Scriitori - cititori
a. prezentarea problemei
b. pseudocod pt preferinta scriitorilor asupra cititorilor
c. modificarile care trebuie facute in pseudocod ca sa aiba cititotorii preferinta asupra
scriitorilor. [ nu mai tin minte care pseudocod trebuia complet scris, dar oricum trebuie stiute
amandoua]
sau
Cautare paralela
a. prezentarea problemei
b. algoritm (parca)
c. complexitate
Varianta
C:
1. Terminarea programelor
2. O problema cu o benzinarie (nu stiu mai multe)
3. Algoritmi unda sau Pram?? si LogP
La Varianta A a dat si S&D cu marcaje
Ce am aflat de la Virgil:
-> s-a dat pe 4 nr
Varianta D
sb1:
Problema generalilor bizantini. Algoritm cu mesaje orale. Complexitatea. + sa rezolve pe
cazul 2 tradatori si 5 generali care nu avea solutie.
sb2: Problema de scris in pseudocod un algoritm cu replicated workers. Aveai o matrice si intr-o
pozitie era o bila si trebuia sa o faci sa ajunga la o alta pozitie din matrice. Erai conditionat ca nu
te puteai deplasa decat intr-o pozitie care avea o valoare mai mica decat a ta. Nu puteai merge pe
diagonala, doar stanga dreapta sus jos.
sb3: La alegere Algoritm de unda LeLang-Chang- Robert si alg tree sau problema producatoriconsumatori de prezentat, de scris algoritm pt comunicare printr-un tampon limitat, alg pt un sg
consumator si un singur producator, pt mai multi si de analizat probleme de sincronizare pe
problema asta.
La prob supl s-a dat un algoritm pipeline in mpi.
La alte numere: O problema cu Replicated Workers, Algoritmul lui Scholten, alg de terminare
prin marcaje, Problema cititori-scriitori, Complexitatea algoritmilor distribuiti (curs 3), Cautarea
paralela, O poza cu un pod si trebuia sa propui un algoritm cum sa treci 5 oameni peste podul ala.
Aveai o lumina care se stingea treptat si trebuia sa-i treci pana nu se stingea lumina (si asasinii
incepeau sa isi aleaga victime :P)
Cam atat. Daca mai aflati subiecte postati aici. ;)
Salut.
Exemple de subecte ce au fost anul trecut:
Un numar:
1: alegerea liderului cu alg ecou: complexitate ,justificare,
descriere problema etc
2: 3 procesoare cu o secventa de nr ordonate crescator, sa alegem
numarul minim comun
3: cititori si scriitori sau producator-consumat or
Altul:
1. Atomicitate si sincronizare
2. n procesoare, fiecare având un numar si trebuia sa afli minimul
3. LeLann chang robert de comparat cu LeeLan
sau
determinarea arborilor de acoperire cu jetoane
S-a dat pe 4 numere.
------------ --------- -------
astea sunt toate:
1. Comunicari sincrone si asincrone prin mesaje
a. prezentarea generala a pb. Cum se face partajarea datelor. Cum se
realizeaza sincroniarea
b. Constructii pseudocod pt transmitere sincrona si asincrona de msg
ex
c. Cum se reprezinta transmiterea sincrona si asincrona a mesajului in
MPI
2. Se da o colectie de procese avand o tipologie de graf conex.
Fiecare proces cunoaste identitatea proprie si identitatile vecinilor.
Scrieti in
pseudocod un algoritm pentru gasirea unei tipoligii conexe cu nr minim
de legaturi intre procese. La terminarea algoritmului fiecare proces
sa cunoasca
identitatile vecinilor cu care a ramas conectat.
3.1 Algoritmul pulsatiilor pentru stabilirea topologiei
Prezentarea Problemei
Descrierea Algoritmului
Complexitate
3.2 Algoritmul pentru detectia terminarii folosind un jeton
Prezentarea problemei pentru procese organizate intr-un grid
Descrierea Algoritmului
Complexitate
V8
1. Alegerea liderului cu algoritmi de unda
1.1 Przentarea problemei. Justificarea folosirii algoritmilor unda
1.2 Descrierea solutiei, algoritm in pseudocod, justificarea
corectitudinii, complexitate
1.3 Ce alte metode de alegere a liderului cunoasteti?
2. Se dau trei procese, fiecare avand o secventa de numere intregi
ordonata crescator. Exista cel putin o valoare comuna celor trei
secvente. Scrieti in
pseudocod algoritmul care gaseste cea mai mica valoare comuna.
Justificati solutia.
3.1 Problema cititorilor si scriitorilor
Prezentarea problemei 0.2p
Descrierea algoritmului 0.5p
Cand este nevoie de acordarea prioritatii cititorilor? Dar
scriitorilor? Justificati. 0.3p
3.2 Problema producator-consumat or cu mesaje sincrone
Prezentarea problemei 0.2p
Descrierea algoritmului 0.5p
Avantaje si dezavantaje fata de solutia cu mesaje sincrone.
0.3p
V9
1. Algoritmi Prefix
1.1 Prezentarea generala a problemei 0.5p
1.2 Solutie pentru gasirea ultimului element dintr-o lista simplu
inlantuita folosind algoritmi prefix, descrierea solutiei in
pseudocod, justificarea
corectitudinii solutiei, analiza complexitatii
1.3 Aplicatie: dati un exemplu pentru o lista de cel putin 4 elemente
2. Descrieti in pseudocod algoritmul distribuit de excludere
mutuala
care functioneaza in modul urmator: un proces care doreste sa intre
in
sectiunea critica trimite mesaje de cerere 'request' tuturor
celorlalte procese. Pentru a putea intra efectiv in sectiunea critica
este necesar sa
primeasca de la fiecare cate un mesaj de raspuns 'reply'. La receptia
unui mesaj 'request' un proces.....sa intre in sectiunea critica. Cand
el are
prioritate, mesajul 'reply' este intarziat... .Analizati complexitatea
algoritmului.
3.1 Complexitatea calcului distribuit: modelul Foster. Exemplificare
prin algoritmul Floyd cu descompunere bidimensionala.
V6
1. Atomicitate si sincronizare
1.1 Prezentare generala a problemei, de ce este nevoie de aceste
concepte...
1.2 Cunstructii pseudocod pt atomicitate si sincronizare, exemple
de...
1.3 Cum se reprezinta atomicitatea in Java? Dar sincronizarea?
2. Se da un tablou de procese M[], fiecare avand initial un numar
intreg...valoarea minima pe care o detine.
3.1 Algoritmul ...-Chang-Robert de stabilire lider
Prezentarea problemei
Descrierea algoritmului
Prin ce difera de algoritmul Lef...?


A linked list is made up of nodes which each have a piece of data and a pointer to the next node. We represent this in Ruby by creating a struct,
institutie: Politehnica Bucuresti
materie: Algoritmi Paraleli si Distribuiti
sesiune: 2013 / Prima sesiune
adaugat de: Laurentiu-Ionut Tuca
materie: Algoritmi Paraleli si Distribuiti
sesiune: 2013 / Prima sesiune
adaugat de: Laurentiu-Ionut Tuca
facultate: Automatica si Calculatoare
profesor: Valentin Cristea
serie / grupa: CA /
data: 2013-02-09
profesor: Valentin Cristea
serie / grupa: CA /
data: 2013-02-09
332CA,334CA - 4.02.2012
Varianta 1
1. Generali bizantini cu mesaje orale. Algoritm plus enunţate teoreme.
2. Problema cu secvenţă critică pentru calcul distribuit. E in notiţe o problema la care trebuie trimise request-uri si reply-uri. De descris alg in pseudocod pt ea.
3a. Ceva java cu synchronized.
3b. Algoritm undă pentru topologie inel.
Varianta 2
1. Stabilirea topologiei cu sondaje cu ecou
2. intr-un graf fiecare nod are o valoare v. Alg pt aflarea maximului dintre aceste valori (la final, fiecare nod stie care e maximul)
3. Complexitate paralela, sau Huang
Varianta 3
1. Algoritmi de tip unda.Algoritmul arbore
2. O problema care se rezolva cu algoritmul pulsatiilor
3. Producator-consumator cu buffer comun de o unitate (la alegere cu Foster).
Varianta 4
1. Producatori - consumatori cu buffer finit
2. O problema care se rezolva cu algoritmul ecou
3. a) Algortimul LaLann - Chang - Robert
b) Nu mai tin minte sigur, stiu ca cerea oricum implementare SIMD si MIMD si diferenta dintre ele
331CA,333CA - 5.02.2013
Varianta 1
1. Ceasuri logice cu solutia lamport (0.8p pt prezentarea problemei si a regulilor) si semafoare distribuite (1.2p idee, mecanisme, pseudocod, se cerea tot ce era prin curs)
2. Aveai n procese intr-un graf conex si un nod putea comunica doar cu vecinii. Se cere ca fiecare nod sa se imperecheze cu un vecin, daca se putea, daca nu, ramanea singur. E acea problema cu imperechere distribuita. Idee 0.3p, pseudocod 0.7
3.1. Suma intr-o retea hipercub de procesoare (nici nu am citit bine ce vroia, cand am vazut hipercub) 3.2. Terminarea intr-o topologie care era un graf cu un ciclu hamiltonian (se facea cu jetoane)
Varianta 2
1. Căutare paralelă: Proprietăți dorite ale algoritmilor paraleli, pseudocod si explicat algoritmul de cautare paralela, complexitate, si de ce nu este buna o simplă paralelizare a cautării binare seriale.
2. Un graf in care fiecare nod își cunoaște vecinii si trebuie sa se afle indicele cel mai mic al nodurilor din graf și să fie transmis nodului inițiator.
3. Producator-Consumator cu buffer limitat folosind P si V la alegere cu complexitatea algoritmilor distribuiti (foster)
Varianta 3
1. Algoritmi unda - algoritmul fazelor.Descrieti problema + justificati folosirea algoritmului unda.Idee algoritm + complexitate + pseudocod.Algoritmul pt clici.
2. Un tablou n/n cu pixeli, fiecare pixel[i][j] apartine unui proces P(i,j) si contine ca valoare intensitatea pixelului. Doi pixeli sunt in aceeasi regiune daca sunt vecini(pe orizontala,verticala) si au ac intensitate. Trebuia sa calculezi minimul indexilor i+j ale proceslor pentru fiecare regiune. Toate procesele trebuie sa stie de acest minim.Idee de rezolvare + rezolvare completa in pseudocod.
3. La alegere intre algoritmul prefixului (bla bla ce se cere) si algoritmi genetici (ceva cu distr calc paralel de genu.. si metoda replicated workers)
Varianta 4
1. Algoritmi de terminare cu marcaje. Descriere (0.5p) Implementare pseudocod + analiză complexitate + corectitudine (1.2p), Comparație cu algoritmul cu mesaje confirmate (0.3p)
2. Problema care calculează diametrul unui graf conex, cunoscând vecinii + nr total de noduri cu un algoritm Heartbeat
3. La alegere intre problema filozofilor si LeLannAlgorithm Examples,
#1: Binary Search
Binary search is an essential search algorithm that takes in a sorted array and returns the index of the value we are searching for. We do this with the following steps:
- Find the midpoint of the sorted array.
- Compare the midpoint to the value of interest.
- If the midpoint is larger than the value, perform binary search on right half of the array.
- If the midpoint is smaller than the value, perform binary search on left half of the array.
- Repeat these steps until the midpoint value is equal to the value of interest or we know the value is not in the array.
From the steps above, it is clear that our solution can be recursive. We will pass in a smaller array to our method on each iteration until our array only contains the value we are interested in. The tricky parts are indexing our array properly and keeping track of our index offset on each iteration so that we can return the index of our value from the original array. See below for our version of the binary search algorithm.
def binary_search(arr, value, offset=0)
mid = (arr.length) / 2
if value < arr[mid] binary_search(arr[0...mid], value, offset) elsif value > arr[mid]
binary_search(arr[(mid + 1)..-1], value, offset + mid + 1)
else
return offset + mid
end
end
Binary search has a time complexity of
O(logn). We know this because if we double the size of our input array, we only need one more iteration of our algorithm to arrive at our final answer. This is why binary search is such a significant algorithm in computer science.Algorithm Examples,
#2: Merge Sort
Merge sort,uses a similar “divide and conquer” methodology to efficiently sort arrays. See the following steps for how merge sort is implemented.
- Return if array is only one element long, because it is already sorted.
- Divide array into two halves until it cannot be divided anymore.

- Merge smaller arrays in sorted order until we have our original sorted array.
To implement merge sort, we will define two methods. One will take care of the splitting up of the array and the other will take care of merging two unsorted arrays back into a single sorted array. We call the dividing-up-method (
merge_sort) recursively until our array is only one element long. We then merge them back together and finally return our sorted array. See below:def merge_sort(array)
return array if array.length == 1
mid_point = array.length / 2
left = array[0...mid_point]
right = array[mid_point..-1]
merge(merge_sort(left), merge_sort(right))
end
def merge(left, right)
merged_arr = []
until left.empty? && right.empty?
if left.length == 0
merged_arr << right.shift
elsif right.length == 0
merged_arr << left.shift
elsif left[0] <= right[0]
merged_arr << left.shift
elsif right[0] <= left[0]
merged_arr << right.shift
end
end
merged_arr
end
Merge Sort has a time complexity of
O(nlogn), which is the best possible time complexity for a sorting algorithm. By dividing and conquering, we dramatically improve the efficiency of sorting, which is already a computationally expensive process.Algorithm Examples,
#3: Adding and Removing From a Linked List
The linked list is a fundamental computer science data structure, that is most useful for it’s constant time insertion and deletion. By using nodes and pointers, we can perform some processes much more efficiently than if we were to use an array. See below for a schematic:

A linked list is made up of nodes which each have a piece of data and a pointer to the next node. We represent this in Ruby by creating a struct,
Node, with two arguments, :data and :next_node. Now, we just have to define two methods, insert_node and delete_node that take in a head node and a location of where to insert/delete. The insert_node method has an additional argument, node, which is the node struct we want to insert. We then loop until we find the location we would like to insert into or delete from. When we arrive at our desired location, and rearrange the pointers to reflect our insertion/deletion.Node = Struct.new(:data, :next_node)
def insert_node(head, node, location)
current_node = head
current_location = 0
until current_location == location
previous_node = current_node
current_node = current_node.next_node
current_location += 1
end
if previous_node
previous_node.next_node = node
node.next_node = current_node
else
node.next_node = current_node
end
head
No comments:
Post a Comment